[科普中国]-希洛夫边界

紧拓扑空间E中若存在紧子集E1，使∑中每个元素f在E1达到最小值且在同类集合中E1为最小，则称E1为E的希洛夫边界。

简介绍凯边界绍凯边界是正则边界点集的一种推广。

设E为紧拓扑空间，∑是从E到(-∞,+∞]的下半连续函数的全体，E的点y称为∑极值点，指的是对E上的任何概率测度μ，不等式对μ中任何元素f成立蕴涵f为狄喇克测度εy。极值点全体称为E（相对于∑）的绍凯边界。

希洛夫边界E中若存在紧子集E1，使∑中每个元素f在E1达到最小值且在同类集合中E1为最小，则称E1为E的希洛夫边界。

性质当D是格林空间Ω的相对紧开集，∑是在D内调和且在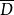上有限连续的函数全体时，D相对于∑的绍凯边界正好是D的正则边界点全体，而它的闭包就是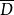的希洛夫边界。这两种边界Ω的紧子集的稳定边界点也有密切关联。1

正则边界点(regular boundary point)

正则边界点是一类边界点。

所谓正则边界点，是指Rn(n≥2)的一个开集ω的边界点x0，使得以∂ω上每个具有紧支集的连续函数f为边界值的广义狄利克雷问题的解在x0的边界值与f(x0)一致，这等价于Rn\ω(或∂ω)在x0不瘦，当n≥3时，这等价于x0为Rn\ω(或∂ω)的2正则点，故可采用维纳判别法(当n=2时，用对数容量代替Cα的类似判别法)。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所