[科普中国]-拟正定核

设对称核 k(x,y) 是G×G上的平方可积函数， K是以k(x,y)为核的线性积分算子。若K仅有有限多个负特征值，则称k(x,y)必是拟正定核。

简介正定核是一类特殊的对称核，其相应的线性积分算子的特征值都是正的。

正定核设对称核 k(x,y) 是G×G上的平方可积函数， K是以k(x,y)为核的线性积分算子。如果K作为映L2(G)入L2(G)的算子，其所有的特征值都是正的，则称k(x,y)是正定核。

定义若K仅有有限多个负特征值，则称k(x,y)必是拟正定核。

对称核线性积分算子特征值对称核线性积分算子特征值是矩阵特征值概念的推广。

设X是巴拿赫空间，T是从X到X中的线性算子，I是X上的恒同算子，λ∈C。若有x∈X，x≠0，使得(λI-T)x=0，则称λ为T的特征值，x称为T相应于λ的特征元（当X是函数空间时，x也可称为T相应于λ的特征函数）。

对于具有对称核k(x,y)的线性积分算子，如果k在G×G上是平方可积的，并且不恒等于0，那么K的特征值与特征函数有很好的性质。1

核(kernel)

核是位势论的基本概念。在位势论中，所谓核，常指一般位势的核。

若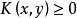恒成立，则称 K 为正核；令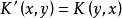（K' 称为 K 的转置核），若 K'=K，则称 K 为对称核；当Ω 为阿贝尔群且有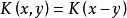时，则称 K 为平移不变核；若对于任意有紧支集的 μ ，有

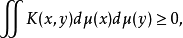则称 K 为正定核，此外，还有各种广义形式的核，如测度核、广义函数核等。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学