[科普中国]-解核

解核是由n次迭核经过求和而得到的一种核。核是位势论的基本概念。在位势论中，所谓核，常指一般位势的核。

简介解核是由n次迭核经过求和而得到的一种核。

设k(x,y)是k(x,y)的n次迭核，λ为实数或复数，则称为解核。

性质设k(x,y)连续，|k(x,y)|≤M，则当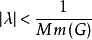时，具有线性积分算子的方程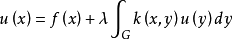存在惟一解，并且该解可以用解核表示为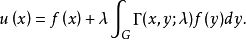

迭核(iterated kernel)

迭核是由已知核经过逐次积分而得到的各种核。

设k(x，y)是线性积分算子的核，令k1(x,y)=k(x,y)，用归纳法定义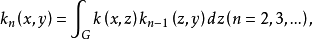：则称kn(x,y)是k(x,y)的n次迭核。1

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学