勒贝格刺是非狄利克雷域的著名例子。勒贝格于1913年给出了具有历史意义的反例,它促使人们进而考虑广义狄利克雷问题。
简介勒贝格刺是非狄利克雷域的著名例子。
在R3的直角坐标系下,XY平面上的曲线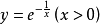 绕x轴旋转的曲面所包围的闭区域F称为勒贝格刺,它在原点瘦。
绕x轴旋转的曲面所包围的闭区域F称为勒贝格刺,它在原点瘦。
推论由此可得到一个与球同胚且边界曲面除O点外充分光滑的区域D,使得D∩F=B\F,其中,B为单位球。
可证D不是狄利克雷域。
意义勒贝格于1913年给出了如上具有历史意义的反例,它促使人们进而考虑广义狄利克雷问题。1
狄利克雷域经典狄利克雷问题亦称第一边值问题,是经典位势论中三大基本问题之一。
经典狄利克雷问题对一般区域未必能求解,使这一经典问题恒能求解的区域称为狄利克雷域。
狄利克雷域的每个边界点都正则。
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国