[科普中国]-实矢量丛

典型纤维为实向量空间Rn，且其结构群为通常的一般线性群GL(n,R)，这样构成的向量丛称为实矢量丛。

简介实矢量丛是一种特殊的向量丛。

典型纤维为实向量空间Rn，且其结构群为通常的一般线性群GL(n,R)，这样构成的向量丛称为实矢量丛。

当n=1时，称为实线丛。1

向量丛向量丛是一个几何构造，对于拓扑空间(或流形,或代数簇)的每一点用互相兼容的方式附上一个向量空间，所用这些向量空间"粘起来"就构成了一个新的拓扑空间(或流形，或代数簇)。

一个典型的例子是流形的切丛：对流形的每一点附上流形在该点的切空间。或者考虑一个平面上的光滑曲线，然后在曲线的每一点附上和曲线垂直的直线；这就是曲线的"法丛"。

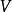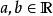实向量空间一个实向量空间是具有两个合成法则的集合（所有及所有）：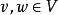

(a)向量加法:；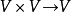

(b)标量乘法：；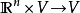

即实数体R上的向量空间叫实向量空间。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学