[科普中国]-埃奇沃斯级数-

埃奇沃斯级数（Edgeworth series）是以爱尔兰经济学家埃奇沃斯来命名的。

简介埃奇沃斯级数（Edgeworth series）是以爱尔兰经济学家埃奇沃斯来命名的。它和 Gram-Charlier A series 一样，是把一个随机变数的机率密度函数展成级数，级数中的每一项是用该随机变数的 cumulants 来表达。对同一个分布，Gram-Charlier A series 和埃奇沃斯级数展出来是同样的级数，只是项的排列不同。（也因此只取前几项作为逼近时的误差会有所不同）

级数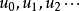在数学中，一个有穷或无穷的序列的元素的形式和S称为级数。序列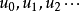中的项称作级数的通项。级数的通项可以是实数、矩阵或向量等常量，也可以是关于其他变量的函数，不一定是一个数。如果级数的通项是常量，则称之为常数项级数，如果级数的通项是函数，则称之为函数项级数。常见的简单有穷数列的级数包括等差数列和等比数列的级数。

有穷数列的级数一般通过初等代数的方法就可以求得。如果序列是无穷序列，其和则称为无穷级数，有时也简称为级数。无穷级数有发散和收敛的区别，称为无穷级数的敛散性。判断无穷级数的敛散性是无穷级数研究中的主要工作。无穷级数在收敛时才会有一个和；发散的无穷级数在一般意义上没有和，但可以用一些别的方式来定义。

无穷级数的研究更多的需要数学分析的方法来解决。无穷级数一般写作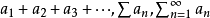，级数收敛时，其和通常被表示为。

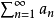Gram-Charlier A级数Gram-Charlier A series 的主要想法，是把待逼近分布（以F为它的密度函数）的特征方程，写成另一个已知分布的特征方程的展式，再经过傅立叶变换的逆变换，就可以求得F的展式。1

假设f是待逼近分布的特征方程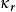，是这个分布的累积量。现在将它展成和另一个已知分布相关的级数。该已知分布的密度函数为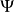，特征函数为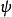，累积量为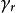。常见的作法是选用正态分布作为已知分布，但事实上选用其它的分布函数也是可行的。由累积量的定义，下列这个等式是恒成立的：

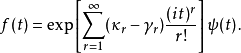
由傅立叶变换的性质，(it)ψ(t) 是 (−1)D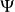(x) 的傅立叶变换，其中D代对x的微分算子。这样我们就得到F的一个级数

如果令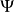为正态分布的密度函数且其期望值和方差与分布F相同，也就是说，期望值 μ = κ1，变异数 σ= κ2，则此展式变成

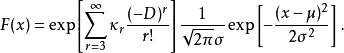
再将指数函数展开并按微分阶数逐项列出，就得到 Gram-Charlier A series。例如，选用正态分布做为已知分布，展到前两项就可以得到

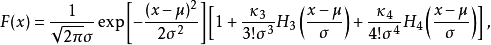
其中H3(x) =x− 3x；H4(x) =x− 6x+ 3 （即埃尔米特多项式）

注意到以上的 series 并不保证函数值恒正，所以事实上并不一定是一个密度函数。在许多情况下，Gram-Charlier A series 会发散—仅当x趋近无限大时F(x) 递降的比 exp(−x/4) 快时它才会收敛 (Cramér 1957)。当它不收敛时，这不是一个真正的渐近展式，因为要估计这个展式的误差是不可能的。因此，一般的情况埃奇沃斯级数比 Gram-Charlier A series 更常用。

Edgeworth扩展的缺点Edgeworth扩展可能会遇到一些问题：

（1）它们不能保证是一个合适的概率分布如下：

密度的积分不需要积分为1，

概率可能是负的。

（2）主要有两个原因，它们可能不准确，特别是在尾部，

它们是围绕平均值的泰勒级数获得的，

它们（渐近地）保证绝对误差，而不是相对误差。当想要近似非常小的量时，这是一个问题，绝对误差可能很小，但相对误差很重要。