[科普中国]-弱可测矢量值函数

弱可测矢量值函数是可测数值函数概念在赋范线性空间上的另一种重要的推广。

简介弱可测矢量值函数是可测数值函数概念在赋范线性空间上的另一种重要的推广。

设(Ω,𝓕,μ)是测度空间，x(t)是定义在Ω上而在赋范线性空间X内取值的向量值函数。如果对任何f∈X*，数值f(x(t))是μ可测的，则称x(t)在Ω上是弱可测的。1

性质强可测函数必是弱可测的，其逆不真。

当X=R1时，强可测、弱可测及实值函数可测这三个概念是等价的。

按弱拓扑连续的函数是弱可测的。

弱可测函数的线性组合是弱可测的。

如果x(t)是弱可测函数，α(t)是有限实值可测函数，则α(t)x(t)亦为弱可测函数。

弱可测函数列关于μ几乎处处弱收敛的极限是弱可测的。

弱可测函数在数学中，特别是泛函分析中，如果一个在巴拿赫空间中取值的函数与其所在空间的对偶空间中的任意元素的复合是一般（强）意义下的可测函数，则该函数是弱可测函数。 对于可分空间，弱可测性和强可测性的概念是一致的。

(X,Σ)是一个可测空间，并且B是域K（通常是实数空间R或复数空间C）上的巴拿赫空间，如果函数f:X→B满足如下条件，对于任意连续线性泛函g:B→K，函数

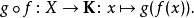是关于Σ和K上一般的波莱尔σ代数的可测函数，则f被称为是弱可测的。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学