n维微分流形 M 上一个开集U到切丛T(M)到映射X,若df∘X=X,则称 X 为关于 f 的不变向量场。
简介向量场向量场是切丛的截面。
n维微分流形 M 上一个开集U到切丛T(M)到映射X,即 X:U→T(M),且满足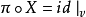 ,特别取 U为M时,称X为M上的向量场。
,特别取 U为M时,称X为M上的向量场。
若 ,则称向量场 X 为光滑向量场。
,则称向量场 X 为光滑向量场。
定义若 是微分流形间的可微映射,定义
是微分流形间的可微映射,定义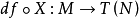 为
为
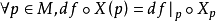 则称它为向量场 X 在df下的像,特别当M=N,f:M→M是一个微分同胚,若
则称它为向量场 X 在df下的像,特别当M=N,f:M→M是一个微分同胚,若 ,则称 X 为关于 f 的不变向量场。1
,则称 X 为关于 f 的不变向量场。1
微分同胚在数学中,微分同胚是适用于微分流形范畴的同构概念。这是从微分流形之间的可逆映射,使得此映射及其逆映射均为光滑(即无穷可微)的。
对给定的两个微分流形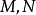 ,若对光滑映射
,若对光滑映射 ,存在光滑映射
,存在光滑映射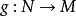 使得
使得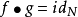 、
、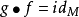 ,则称为微分同胚。此时逆映射
,则称为微分同胚。此时逆映射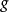 是唯一的。
是唯一的。
若在微分流形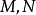 之间存在微分同胚映射,则称
之间存在微分同胚映射,则称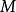 与
与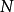 是微分同胚的。
是微分同胚的。
可微映射设D是Rn中的一个区域,f:D→Rn是以D为定义域的映射,如果f在D上的每一点处可微,则称f为D上的可微映射。
设D是 中的一个区域,
中的一个区域,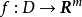 是以D为定义域的映射,
是以D为定义域的映射,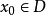 ,如果对于自变量
,如果对于自变量 的增量
的增量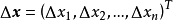 ,因变量
,因变量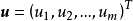 的增量
的增量 可以分解为
可以分解为
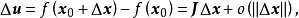 其中
其中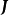 是一个
是一个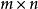 阵,
阵,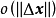 是m维空间
是m维空间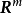 中的向量,它的各分量均是比
中的向量,它的各分量均是比 高阶的无穷小量,则称映射
高阶的无穷小量,则称映射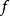 在
在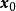 点可微。
点可微。
本词条内容贡献者为:
胡启洲 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国