坐标丛在严格等价之下的一个等价类称为一个纤维丛。由于每一个坐标丛都惟一地决定了一个纤维丛,故通常当得到一个坐标丛时,就认为得到了一个纤维丛,且简记为(E,B,π,F,G)。
简介设空间 E 称为全空间,空间 B 称为底空间,连续映射π:E→B 称为投影,空间 F 称为典型纤维,G 位作用在F上的有效拓扑变换群,称为结构群,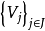 为B的开覆盖,且对每个 Vj 有同胚
为B的开覆盖,且对每个 Vj 有同胚
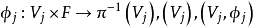 称为局部平凡化区图,而
称为局部平凡化区图,而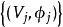 称为图册,若满足下列条件,它就是一个坐标从:
称为图册,若满足下列条件,它就是一个坐标从:
1、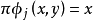 ,对任意
,对任意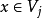 和任意 y∈F;
和任意 y∈F;
2、令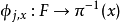 为
为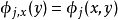 ,则对任意
,则对任意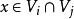 ,同胚
,同胚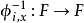 ,属于 G;
,属于 G;
3、对任意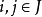 ,由
,由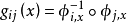 定义的映射
定义的映射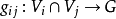 连续,
连续,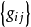 称为转移函数族,
称为转移函数族,
表示方法坐标丛记为
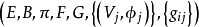 对任意 x∈B,记
对任意 x∈B,记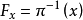 ,称为点x上的纤维,它同胚于典型纤维F。
,称为点x上的纤维,它同胚于典型纤维F。
性质若两个具有相同的全空间、底空间、投影、典型纤维和结构群的坐标丛的两个转移函数族合并起来仍满足条件1,2和3,即仍成为一个转移函数族,则称这两个坐标丛严格等价。
坐标丛在严格等价之下的一个等价类称为一个纤维丛。
由于每一个坐标丛都惟一地决定了一个纤维丛,故通常当得到一个坐标丛时,就认为得到了一个纤维丛,且简记为(E,B,π,F,G),当G无需指明时也简记为(E,B,π,F),当F,G和π无需指明时也说E是B上的一个纤维丛。例如,若M是n维微分流形,其切丛T(M)在自然投影π之下是M上的一个纤维丛,实际上是以T(M)为全空间,M为底空间,π为投影,Rn为典型纤维,一般线性群 GL(n,R)为结构群的纤维丛。1
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国