BMO范数(BMO norm)记为||f||∗,其中,BMO是有界平均振动之意。
简介BMO函数空间BMO函数空间是一类函数空间,BMO是有界平均振动之意。
设 f 是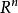 上的局部可积函数,Q表示
上的局部可积函数,Q表示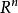 中的边与坐标轴平行的立方体,记
中的边与坐标轴平行的立方体,记
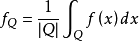 (|Q| 为 Q 的体积).
(|Q| 为 Q 的体积).
设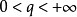 ,如果 f 满足
,如果 f 满足
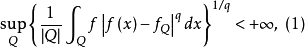 则称f是q 次有界平均振动的,这样的函数全体记为
则称f是q 次有界平均振动的,这样的函数全体记为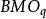 ,由于对所有q>0,
,由于对所有q>0,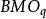 都互相等价,故可简记为BMO,并称它为BMO的函数空间。
都互相等价,故可简记为BMO,并称它为BMO的函数空间。
BMO是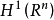 对偶空间,可以证明
对偶空间,可以证明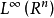 空间同BMO有着严格的包含关系:
空间同BMO有着严格的包含关系: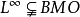 。
。
定义如记
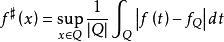 则定义中的条件
则定义中的条件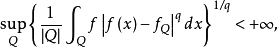 等价于
等价于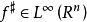 ,因此
,因此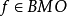 当且仅当
当且仅当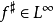 ,函数
,函数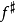 称为 f 的#函数,对于
称为 f 的#函数,对于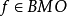 ,当 q=1时,公式左端的数称为 BMO范数,记为
,当 q=1时,公式左端的数称为 BMO范数,记为 。1
。1
范数(norm)
范数是数学中的一种基本概念。
在泛函分析中,它定义在赋范线性空间中,并满足一定的条件,即①非负性;②齐次性;③三角不等式。它常常被用来度量某个向量空间(或矩阵)中的每个向量的长度或大小。
范数是一个函数,是矢量空间内的所有矢量赋予非零的正长度或大小。半范数可以为非零的矢量赋予零长度。
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国