[科普中国]-马钦凯维奇乘子定理

马钦凯维奇乘子定理（Marcinkiewicz multiplier theorem）是给出数列为Lp(p>1)乘子的定理。

简介马钦凯维奇乘子定理是给出数列为Lp(p>1)乘子的定理。

它断言：若数列{λk}满足条件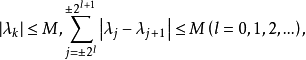则对一切p>1，{λk}是Lp乘子。1

乘子乘子是一种由特殊数列决定的算子。

设P,Q分别为任意两个周期为2π的函数类，{λk|k=0,±1,±2,...}是一个数列。如对于P中任一函数f的傅里叶系数{ck|k=0,±1,±2,...}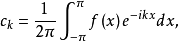：数列{ckλk|k=0,±1,±2,...}总是Q中某个函数g的傅里叶系数，即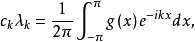这样，数列{λk}确定了一个将f∈P映到g∈Q的算子T，使得Tf=g，此时称T为(P,Q)乘子，也称{λk}为(P,Q)乘子。

数列数列（sequence of number）是以正整数集（或它的有限子集）为定义域的函数，是一列有序的数。

数列中的每一个数都叫做这个数列的项。排在第一位的数称为这个数列的第1项（通常也叫做首项），排在第二位的数称为这个数列的第2项，以此类推，排在第n位的数称为这个数列的第n项，通常用an表示。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学