[科普中国]-ε连续集值映射

ε连续集值映射（ε-continuous setvalued mapping）是同时为ε上半连续与ε下半连续的映射。

简介ε连续集值映射是同时为ε上半连续与ε下半连续的映射。

ε上半连续集值映射(ε-upper semicontinuous setvalued mapping )

ε上半连续集值映射对度量空间中的集值映射提出的一种特殊的上半连续性概念。

设X是拓扑空间，(Y,d)为度量空间。F:X→2Y是集值映射，x0∈X。若对于任给的ε>0，存在x0的邻域U，使得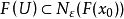其中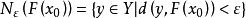，则称F在x0为ε上半连续。

若F在X中的每一点均为ε上半连续，则称F:X→2Y为ε上半连续。若F在x0上半连续，则F在x0为ε上半连续。当F(x0)为紧集时，反之亦真。

ε下半连续集值映射(ε-lower semicontinuoussetvalued mapping)

ε下半连续集值映射对度量空间中的集值映射提出的一种特殊的下半连续性概念。

设X是拓扑空间，(Y ,d)是度量空间。F:X→2Y是集值映射，x0∈X。若对于任给的正数ε，存在x0的邻域U，使得F(x0)⊂Nε(F(x))(∀x∈U)，则称F在x0为ε下半连续。

若F在X中的每一点均为ε下半连续，则称F:X→2Y为ε下半连续。F在x0为ε下半连续→F在x0下半连续。当F(x0)是紧集时，其逆亦真。1

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学