[科普中国]-流形上微分算子理论

流形上微分算子理论是流形上的分析的一个分支，它研究流形上椭圆微分算子及拟微分算子的阿蒂亚-辛格指标定理及其应用。

简介流形上微分算子理论是流形上的分析的一个分支，它研究流形上椭圆微分算子及拟微分算子的阿蒂亚-辛格指标定理及其应用。

线性微分算子设M是紧可定向流形，E，F是M上的C∞复向量丛，线性映射P:C∞(E)→C∞(F)，其中C∞(E)与C∞(F)分别是E与F的C∞截面构成的复向量空间，若在局部坐标下P表示为向量微分算子，则称P为M上的线性微分算子。类似地可定义M上的拟微分算子。

椭圆算子对于这两种算子，可以定义丛同态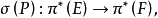σ(P)是算子P的象征。若象征是同构的话，微分算子（或拟微分算子）P就是椭圆算子。

阿蒂亚-辛格指标对于椭圆算子，阿蒂亚-辛格指标定理指出：椭圆算子的指标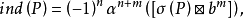其中αn+m是博特同构的迭代，b是贝蒂类，⊠是外积。

这个定理有三种证明方法：配边证明、嵌入证明和热方程证明。

应用阿蒂亚-辛格定理有极广泛的应用，能包容高斯-波涅公式、希策布鲁赫符号差定理、黎曼-罗赫-希策布鲁赫定理；推出莱夫谢茨公式及更广泛的阿蒂亚-博特-莱夫谢茨数公式；能应用于有边界的紧流形的椭圆型边值问题，还可应用于规范场理论等。

发展指标定理是阿蒂亚(Atiyah,M.F.)与辛格(Singer,I.M.)于1963年的一篇合作论文中首先发表的，继而于1968年阿蒂亚和辛格又给出了指标定理的上同调形式。

阿蒂亚-辛格指标定理是分析学与拓扑学结合的范例。1

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所