[科普中国]-仓西定理

仓西定理（Kuranishi theorem）是某些条件保证Rn中拟微分算子写成有紧支集的拟微分算子的定理。

简介概述仓西定理是某些条件保证Rn中拟微分算子写成有紧支集的拟微分算子的定理。

具体内容设U⊂Rn是开集，k∈Z，考察形如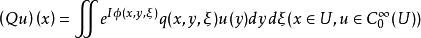的算子，其中“振幅”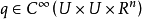满足下述条件：

1、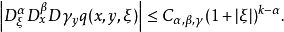

2、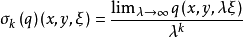对ξ≠0存在。

3、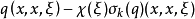是U上k-1阶标准拟微分算子的振幅（𝛘是截段函数）。

4、q(x,x,ξ)关于变量x,y有紧支集，相函数𝜙定义于U×U×Rn上是实值的，关于变量ξ是线性的，对ξ≠0是C∞的及对固定的x（或y）没有临界点(y,ξ)（或(x,ξ)），进而假设则Q可以写成一个具紧支集的拟微分算子。1

拟微分算子拟微分算子是一类由积分形式确定的算子，与微分算子有类似的性质。

在拟微分算子中，适当可支的拟微分算子起重要作用。所谓一个拟微分算子是适当可支的，是指它的核在X×X中的支集到X上的两个投影是适当映射。

线性微分算子是一类特殊的拟微分算子，其振幅是ξ的多项式；线性椭圆微分算子的拟基本解也是拟微分算子，其振幅是一个渐近展开式；希尔伯特变换是一个零阶的(1,0)型拟微分算子。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所