[科普中国]-黎曼-罗赫-希策布鲁赫定理

把指标定理应用于铎尔博尔复形就得出黎曼-罗赫-希策布鲁赫定理（Riemann-Roch-Hirzebruch therorem）。

简介把指标定理应用于铎尔博尔复形就得出黎曼-罗赫-希策布鲁赫定理。

背景设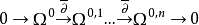是n维克勒流形的铎尔博尔复形，Ω0,p表示p次复外微分形式空间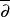，是外导数。若V是X上一个全纯向量丛，则可构造广义铎尔博尔复形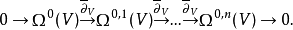

定义欧拉示性数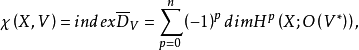其中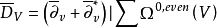是一阶椭圆算子，而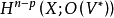是系数在V*中全纯截面的芽层X的n-p维上同调。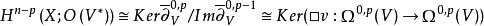这里的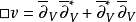。≅系数在V中的X上p次整体全纯微分形式的空间。

定理内容由上可得出黎曼-罗赫-希策布鲁赫定理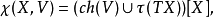ch(V)是V的陈特征，τ(TX)是X的Todd类。

特殊情况当V是平凡的线丛CX，则𝛘(X)=𝛘(X,V)称为X的算术亏格，有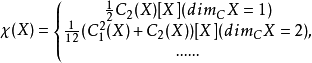其中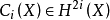是TX的第i个陈类。1

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所