[科普中国]-贝叶斯搜索理论

贝叶斯搜索理论利用贝叶斯统计理论搜索失踪物，曾被多次用于搜救失踪的船只。

流程一般的流程如下：1

提出所有关于船只失踪事件的假设。

针对每一假设，构造船只位置的空间分布概率。

针对每一位置，假设已知船只位于此处，计算能找到失踪船只的概率分布。在海洋中，这一般取决于水深：在浅水处找到失踪物的机会比在深水处大。

结合上述两个概率分布，构造整体的搜索成功的概率分布。

构造搜索路径：始于高概率区，经过居中概率区，最后搜索低概率区。

在搜索过程中，持续更新上述概率分布。例如，如果在某处未能找到失踪物，那么船只位置分布于此的概率要被降低。这一更新过程需要用到贝叶斯定理。

贝叶斯搜索不仅可以综合多个信息来源，而且可以自动估计搜索成功的概率。即使在搜索前，我们可以估计“5天内找到失踪物的概率是65%。在搜索十天后，这个概率会升高到90%。15天后，升高到97%”。如此，在分配搜索资源前可以评估可行性。

数学假定失踪物位于某区域的概率是 p，在此处能搜索成功的概率是 q。如果搜索此处后未能找到失踪物，根据贝叶斯定理，失踪物位于此处的概率被更新为

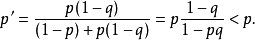
对其它区域，如果其原本失踪物在其处的概率是 r，那么这一概率将被更新为

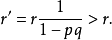
另见贝叶斯推断

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学