[科普中国]-最大离散熵定理

最大离散熵定理(maximal discrete entropytheorem)离散信源的熵达到最大值的一个重要定理。

简介该定理断言:对于具有q个符号的离散信源，当q个信源符号出现的可能性相等时，信源的嫡达到最大值，即

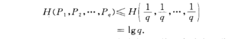称信源中的事件为等概率事件。即等概率分布的信源其平均不确定性最大。

最大熵原理最大熵原理是一种选择随机变量统计特性最符合客观情况的准则，也称为最大信息原理。随机量的概率分布是很难测定的，一般只能测得其各种均值（如数学期望、方差等）或已知某些限定条件下的值（如峰值、取值个数等），符合测得这些值的分布可有多种、以至无穷多种，通常，其中有一种分布的熵最大。选用这种具有最大熵的分布作为该随机变量的分布，是一种有效的处理方法和准则。这种方法虽有一定的主观性，但可以认为是最符合客观情况的一种选择。在投资时常常讲不要把所有的鸡蛋放在一个篮子里，这样可以降低风险。在信息处理中，这个原理同样适用。在数学上，这个原理称为最大熵原理。

从这个意义上讲，那么最大熵原理的实质就是，在已知部分知识的前提下，关于未知分布最合理的推断就是符合已知知识最不确定或最随机的推断，这是我们可以作出不偏不倚的选择，任何其它的选择都意味着我们增加了其它的约束和假设，这些约束和假设根据我们掌握的信息无法作出。

相关研究一种结合图像离散熵和自组织神经网络的边缘检测方法。首先，用离散熵选定阈值来分割图像的平滑区域和灰度变化剧烈的区域，用来减少计算量；其次将灰度图像转化为理想二值像素模式；定义了6个边缘类型和6个原型向量。将这些边缘向量作为神经网络的输入，通过SOM对其进行边缘分类从而获得边缘图像。最后将斑点边缘从边缘图像中去除即得到理想的边缘图像1。

公共重点区域的智能监视问题，提出了一种新的徘徊行为异常检测方法。该方法利用视频目标跟踪算法得到可疑行人的运动轨迹，通过曲线拟合对运动目标的离散点轨迹进行平滑，计算离散点的离散曲率，计算感兴趣区域内运动目标轨迹点的离散曲率的熵及方差，通过离散熵阈值比较进行徘徊行为判断2。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学