[科普中国]-抽象逼近

在泛函分析的框架下，应用巴拿赫空间几何、非线性分析等理论来讨论度量空间中某一子集对某一确定的元素的逼近，称为抽象逼近。

简介抽象逼近是抽象空间中的逼近论问题。

在泛函分析的框架下，应用巴拿赫空间几何、非线性分析等理论来讨论度量空间中某一子集对某一确定的元素的逼近，称为抽象逼近。

推广设X是距离空间，其元素（或者称为点）x与y之间的距离记为ρ(x,y)。设G是X的一个子集，称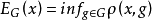为x与G之间的距离，它自然标志着G对x的逼近程度，常称它为G对x的最佳逼近值，又称G为逼近集。倘若G中有元素g0使得ρ(x,g0)=EG(x)，则称g0为x在G中的最佳逼近元。

主要内容在一般的距离空间中，人们研究的逼近理论主要还是定性问题。就是如下四方面的问题：

1、x在G中的最佳逼近元的存在性问题。也就是说，记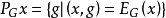，即PGx是x在G中的最佳逼近元的全体，PGx是不是空集？

2、x在G中的最佳逼近元存在的话，是否惟一？这就是常说的惟一性问题。

3、最佳逼近元的特征刻画。

4、如果将PG看做X中元素x到X的子集PGx的一个映射，那么一个重要的问题是集值映射PG有什么性质。

发展在巴拿赫空间中抽象逼近已有较丰富的成果，而对非巴拿赫空间中的研究尚在发展中。1

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学