[科普中国]-希尔伯特-施密特积分算子

希尔伯特-施密特积分算子（Hilbert-Schmidtintegral operator）是一类核平方可积的积分型算子。

简介希尔伯特-施密特积分算子是一类核平方可积的积分型算子。

有界线性算子设(x,y)是测度空间，K(s,t)是(Ω×Ω,𝓑×𝓑,μ×μ)上可测函数，并且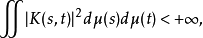则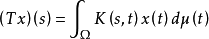是L2(Ω,𝓑,μ)到自身的有界线性算子。

定义如果L2(Ω,𝓑,μ)是可分空间，那么易知T是L2(Ω,𝓑,μ)上的希尔伯特-施密特算子。因而上述积分算子通常称为希尔伯特-施密特积分算子。1

希尔伯特-施密特算子设H是可分的希尔伯特空间，𝓚(H)是H上的紧算子全体，对于 T∈𝓚(H)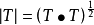，也是紧的，设其特征值按大小顺序为α1≥α2≥...≥αn≥...（按重复度重复编号），𝓚(H) 中满足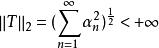全体记为C2(H) ，简记为C2，称为 H 上的施凯特2类。

C2类算子被称为希尔伯特-施密特算子，而相应的范数‖·‖2称为希尔伯特-施密特范数。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学