[科普中国]-希尔伯特-施密特定理

希尔伯特-施密特定理是对称核线性积分算子的基本定理，是希尔伯特(Hilbert,D.)和施密特(Schmidt,E.)所建立的。这一定理在对称核线性积分方程理论中起重要作用。

简介希尔伯特-施密特定理是对称核线性积分算子的基本定理。

设K是对称核线性积分算子，其核k(x,y)是平方可积的，并且不恒等于零。设{λn}和{ψn}是K的全系特征值与全系就范正交特征函数。设h(x)是平方可积的，令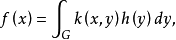则f(x)可以表示为{ψn}的几乎绝对一致收敛的傅里叶级数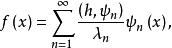并且若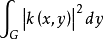有界，则上述收敛是绝对一致收敛。

应用希尔伯特-施密特定理是希尔伯特(Hilbert,D.)和施密特(Schmidt,E.)所建立的。这一定理在对称核线性积分方程理论中起重要作用。

有时，人们还把关于对称核线性积分算子的一整套理论也统称为希尔伯特-施密特理论。1

对称核线性积分算子(linear integral operator with symmetric kernel)

对称核线性积分算子是具有对称核的线性积分算子，又称为具有埃尔米特核的线性积分算子。对称核线性积分算子理论，是有限维空间对称矩阵理论在无穷维空间的推广。

1904年，希尔伯特(D.Hilbert)从有限维空间对称矩阵理论出发，通过取极限的方法，最早进行了对对称核线性积分算子的研究，施密特(E.Schmidt)等也做出了重要贡献。对称核线性积分算子的理论在近代已经被抽象和推广为希尔伯特空间上的自共轭算子的谱分解理论。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学