[科普中国]-维塔利-维纳覆盖引理

维塔利-维纳覆盖引理（The Vitali-Wiener covering lemma ）是覆盖引理的一种形式。

简介维塔利-维纳覆盖引理是覆盖引理的一种形式。1

设区域Ω⊂Rn，且|Ω|0，使得球B(x,r(x))⊂Ω，则存在序列{B(xi,r(xi))}i，使得诸球B(xi,r(xi))互不相交，且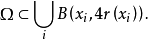

维塔利覆盖引理数学上，维塔利(Vitali)覆盖引理是一个组合几何的结果，用于实分析中。

维塔利覆盖引理说给出一族球，可以从中找到互不相交的球，将这些球半径增加一定倍后，就能把其他的球都覆盖住。

维纳型覆盖引理(covering lemma of Wienertype)

维纳型覆盖引理是局部域上的一个覆盖引理。

局部域K有一个与Rn迥然不同的性质：K中任意两个球S与T只可能有以下两种不同的相对位置。即：

1、S∩T=∅，

2、S⊂T或T⊂S。

据此可以证明维纳型覆盖引理：设E⊂K是K的哈尔可测子集，且|E|