[科普中国]-复化线性映射

复化线性映射（complexified linear map）是复向量空间间的线性映射被复化。

简介复化线性映射是复向量空间间的线性映射被复化。

设E,F是复向量空间，A∈LR(E,F)，A的复化为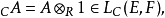则称CA是复化线性映射。1

线性映射在数学中，线性映射（也叫做线性变换或线性算子）是在两个向量空间之间的函数，它保持向量加法和标量乘法的运算。术语“线性变换”特别常用，尤其是对从向量空间到自身的线性映射(自同态)。

在抽象代数中，线性映射是向量空间的同态，或在给定的域上的向量空间所构成的范畴中的态射。

向量空间向量空间又称线性空间，是线性代数的中心内容和基本概念之一。在解析几何里引入向量概念后，使许多问题的处理变得更为简洁和清晰，在此基础上的进一步抽象化，形成了与域相联系的向量空间概念。譬如，实系数多项式的集合在定义适当的运算后构成向量空间，在代数上处理是方便的。单变元实函数的集合在定义适当的运算后，也构成向量空间，研究此类函数向量空间的数学分支称为泛函分析。

向量空间它的理论和方法在科学技术的各个领域都有广泛的应用。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所