[科普中国]-欧拉-拉格朗日定理

欧拉-拉格朗日定理（Euler-Lagrange theorem）是把条件极值化归为没有约束条件的极值的一个定理。

简介欧拉-拉格朗日定理是把条件极值化归为没有约束条件的极值的一个定理。

具体内容欧拉-拉格朗日定理断言：若函数（或曲线）y(x)在条件及边界条件之下，给泛函以极值，且若y(x)是满足条件的泛函J的平稳函数，则存在这样一个常数λ，使y(x)是泛函的平稳函数，其中H=F+λG。常数λ称为欧拉-拉格朗日常数。1

条件极值条件极值是泛函J在某附加条件下的极值。

例如，泛函

函数y，z除满足固定边界条件y(x0)=y0， y(x1)=y1， z(x0)=z0， z(x1)=z1之外还满足一个附加条件

或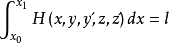这种问题的极值称为条件极值。

本词条内容贡献者为:

杨荣佳 - 教授 - 河北大学