[科普中国]-拉格朗日插值多项式逼近

拉格朗日插值多项式是一种最常见的多项式插值法，也是一种最常用的逼近工具。

简介拉格朗日插值多项式逼近是常用的逼近工具。

拉格朗日插值多项式设 是 [a,b] 上 n 个互异的点，1795年，拉格朗日就证明：如果定义在[a,b]上的函数 f(x) 在 xk 处的值数不高于 n 的代数多项式Ln(f,x),使得Ln(f,xk)=f(xk)(k=1,2,...,n)，倘若记

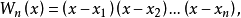
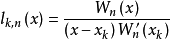则有

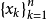等式(1) 中的 称为 f(x)的拉格朗日插值多项式，并称 为其结点组，而称 为拉格朗日插值基本多项式。

具体内容若f(x)是次数不高于 n-1 度代数多项式，则 的几何意义是有且仅有一条n-1次代数曲线通过平面上预先给定的n个横坐标互异的点，对于 [a,b]上的连续函数f(x)， 是一个可计算的逼近工具，若f(x)有r阶连续导数，则

其中ξ是[a,b]中一个与x有关的点

对于给定的结点组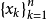 ，称

为此结点组的勒贝格函数，而称 为其勒贝格常数，如果记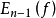 为次数不高于 n-1度代数多项式对函数 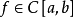的最佳逼近值，则有

而且有。

因此，选择λn取值小的结点组是一个重要的工作，但是，对于[a,b]上的任一结点组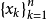费伯与伯恩斯坦分别于1914年与1916年证明了

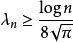于是人们只能选择阶接近log n 的结点组，最常用的于是在[-1,1]上取切比雪夫多项式

的零点全体

作为结点组，此时相应的勒贝格常数不超过

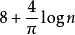因此，只要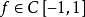 的连续性模 适合条件

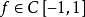就可以保证 n→∞时， 在 [-1,1]上一致收敛于 f(x)，如果 有r阶连续导数，那么不等式

成立，其中Cr>0仅与 r 有关。

推广关于插值多项式的逼近不仅考虑一致逼近，还可考虑平均逼近，Lp 度量下的逼近等。

关于插值结点组，不仅限于切比雪夫多项式的零点，而且还可取一般正交多项式的零点，这里零点的分布情况是十分要紧的，然而，倘若取均匀分布的结点，那么其结果往往是不好的。例如，即使对于像

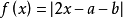这样很好的函数，其等距结点组上的拉格朗日插值多项式也不能在[a,b]上实现对他的逼近。1

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学