[科普中国]-ε覆盖

对于给定的ε> 0，A的ε覆盖中集Uk的个数n是与这个集族的选取有关的。

简介设 X 是巴拿赫空间，x∈X，‖x‖表示 x 的范数，A 是X的紧子集，ε>0 是给定的正数，如果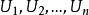是 X 的一族子集，每个 Uk的直径都不超过 2ε，亦即

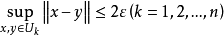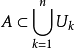而且那么称集族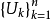是A的一个ε覆盖。

推广对于给定的ε> 0，A的ε覆盖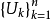中集Uk的个数n是与这个集族的选取有关的，但n的最小值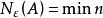却是一个仅与ε有关的关于集A的不变量，即当A给定后，Nε(A)是一个仅与ε有关的非负整数，人们称数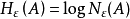为集A的熵，或者区别于概率论中的同名概念，称Hε(A)为集A的度量熵。

ε网设X是巴拿赫空间，A是X的紧子集，ε>0是给定的正数，如果X中存在有限个点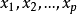,使得对于每个点x∈A，都至少有xk使得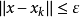，也即x与xk的距离ρ(x,xk)不超过ε:ρ(x,xx)≤ε，则称集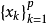为A的一个ε网。

集A的ε网中点的个数p在ε>0给定后，自然与这些点的取法有关。但是p的最小值Pε(A) = min p却是集A的一个不变量。它当然与空间X有关，称数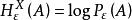为A关于X的熵。1

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学