[科普中国]-斯米尔诺夫区域

斯米尔诺夫区域是一种与多项式系完备性相关的区域。使多项式系在Ep(G)中完备的充分必要条件是，区域G为斯米尔诺夫区域。

简介斯米尔诺夫区域是一种与多项式系完备性相关的区域。

设G是有界单连通区域，其边界曲线C是若尔当可求长曲线，z=Ψ(ω)是将|ω|0，Ep(G)={f(z)|f(z)在G内解析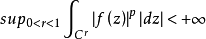，}，其中Cr是C的内等势线。若ψ(ω)满足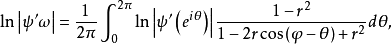其中ω=reiθ,0≤r0。

完备性是指在数学及其相关领域中，当一个对象具有完备性，即它不需要添加任何其他元素，这个对象也可称为完备的或完全的。

完备性也称完全性，可以从多个不同的角度来精确描述这个定义，同时可以引入完备化这个概念。完备性在一般空间中表示任何空间中的柯西点列的一致收敛极限包含于这个空间中。完备性与所定义的度量有关，一旦定义了度量，那么可以讨论这个空间的完备性。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学