[科普中国]-仿线性化

仿线性化是对于非线性函数F(x,y)进行线性化，使其成为仿积与具更高正则性余项之和的方法。

简介仿线性化是对于非线性函数F(x,y)进行线性化，使其成为仿积与具更高正则性余项之和的方法。

设F(x,y)是Rn×RN上的C∞函数，x=(x1,x2,...,xn)∈Rn，y=(y1,y2,...,yn)∈RN，且它的各阶导数在K上有界，K为Rn×RN中的任意紧集，则对实uj(x)=Cρ(Rn)(p>0,j=1,2,...,N)，有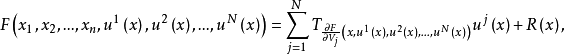其中R(x)∈C2ρ(Rn)。又若uj(x)∈Hs(Rn)(s>n/2)，则。

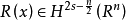上述结果表明，对非线性函数F(x,y)可用上述一种特殊的线性化方法化成仿积及正则性更高的余项之和。这种线性化方法称为仿线性化。

应用在处理具体问题时还可出现各种不同的仿线性化形式。利用上述仿线性化，可以将非线性微分方程经过线性化而用仿微分算子来表示。

实例考察m阶完全非线性微分方程F(x,u,...,∂βu,...)|β|≤m=0。设F关于它的自变量为C∞。记N为上述β取遍|β|≤m的全体的个数。设F及各阶导数在紧集K⊂Rn×RN上有界。又设u(x)是方程的Cρ+m实解，ρ>0（或Hs+m,s>n/2），则用上述仿线性化可将方程化为Pu=R(x)。此处R(x)∈C2ρ（或H2S-n/2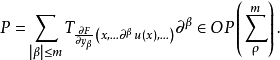），它的主象征是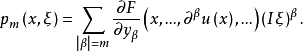当方程为拟线性或半线性时，u(x)的光滑性可减弱，R(x)的光滑性可提高。这样非线性微分方程问题就归结为仿微分方程的问题了。1

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学