[科普中国]-外尔斯特拉斯条件

外尔斯特拉斯条件是变分积分取强极值的一个必要条件。这个条件是外尔斯特拉斯(Weierstrass,K.(T.W.))于1879年提出的。

简介外尔斯特拉斯条件是变分积分取强极值的一个必要条件。

若y*使泛函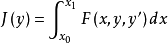 取强极小值，则对所有x∈(x0,x1),q∈R1，外尔斯特拉斯E函数满足 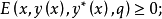相应地，对强极大值有 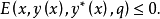这个条件是外尔斯特拉斯(Weierstrass,K.(T.W.))于1879年提出的。1

应用对一元向量函数u(x)对应对拉格朗日函数，外尔斯特拉斯条件是对任意的x∈Ω和秩为1的矩阵π， 其中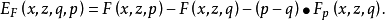

外尔斯特拉斯E函数外尔斯特拉斯E函数是表述强极值必要条件的一个函数。

泛函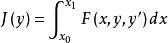的外尔斯特拉斯E函数（4个变量的函数）是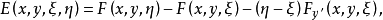又称E函数。

强极值(strong extremism)

强极值是在连续函数集中取得的极值。

如果泛函J(y)在某个函数y0的某个零级邻域上取得极值，那么这个极值称为强极值。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学