[科普中国]-诺特方程

y 是 J 的内平稳函数，每个内平稳函数满足方程，则这个方程称为诺特方程。

简介内变分内变分是变分积分相对于未知函数的自变量的变化的变化率。

对一维情形，设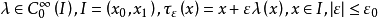（ε0是适当小的正数）使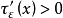，令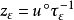，若 y 是泛函

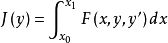的极值函数，则应有

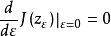称上式为泛函 J 在 y 的沿λ 方向的（一阶）内变分，记为。

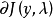定义若一个函数 y 使对任意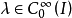有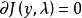，则称 y 是 J 的内平稳函数，每个内平稳函数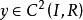满足方程

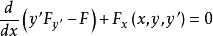这个方程称为诺特方程。

性质对一般的变分积分

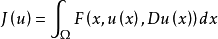设被积函数 F(x,z,p)在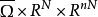上有一阶连续微商，令

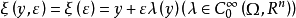这时称

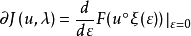为泛函 J 在 u 的沿方向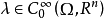的（一阶）内变分。1

推论由

定义哈密顿张量（能量一动量张量）

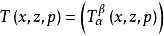则

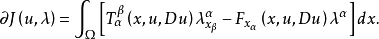
本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学