[科普中国]-最小位能原理

从哈密顿原理可以等价地推出相应的质点组的运动方程，通常是微分方程。如果力学系统处于静力平衡稳定状态，则因动能为零，位能与时间无关，哈密顿原理转化为最小位能原理。

简介哈密顿原理哈密顿原理亦称最小作用原理，是力学中的一个变分原理。

拉格朗日函数L是质点组的动能与势能之差，即L=T-V，T为动能，V为势能。哈密顿原理断言：在一切容许的运动中，质点组的真实运动满足积分 有极值的必要条件δJ=0。

定义如同一般变分原理一样，从哈密顿原理可以等价地推出相应的质点组的运动方程，通常是微分方程。如果力学系统处于静力平衡稳定状态，则因动能为零，位能与时间无关，哈密顿原理转化为最小位能原理：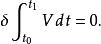

应用在力是保守力的情况下，对任何有限粒子组，对于更一般的动力系统以及连续介质，这一原理的推广同样适用。1

弹性理论中的最小位能原理弹性理论中的最小位能原理是用应变变分表示的弹性力学变分原理。

对于给定的弹性体，真实发生的位移使体系总位能的一次变分为零。记位移为u=(u1,u2,u3)，应变为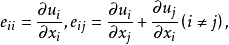应力为σij，体积力密度为F=(F1,F2,F3)，表面力密度为P=(P1,P2,P3)，体系总位能为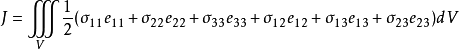

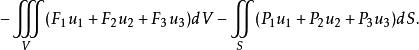
以位移变分表示位能的变分，则有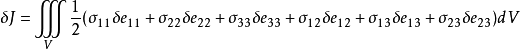

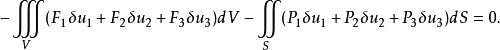
本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学