从数学意义上,最优控制过程可分为三类:拉格朗日问题、麦耶尔问题和波尔扎问题。
如果已知系统的状态方程与初始状态,要求最优控制u(t),使得相应的积分型指标为极小,这样的最优控制问题叫做拉格朗日问题。1
定义我们知道最优控制理论是泛函求解极值问题。泛函三种典型问题分别为:拉格朗日问题、麦耶尔问题和波尔扎问题。
拉格朗日问题(Lagrange problem)的具体表述如下:
给定状态方程
 与初始条件
与初始条件
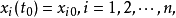 泛函取以下形式
泛函取以下形式
 其中
其中 为
为 维状态向量,
维状态向量, 为
为 维控制向量,
维控制向量,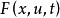 是
是 的连续函数。
的连续函数。
拉格朗日问题要求从可供选择的函数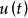 中确定出一个
中确定出一个 ,在上述状态方程约束和初始条件下使泛函
,在上述状态方程约束和初始条件下使泛函 取极小值。2
取极小值。2
麦耶尔问题给定上述状态方程和初始条件,及以下的终端条件
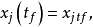 要求的系统目标函数泛函为:
要求的系统目标函数泛函为:
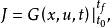 麦耶尔问题要求从可供选择的函数确定出一个
麦耶尔问题要求从可供选择的函数确定出一个 ,在上述状态方程约束和初始条件下使泛函取值极小。12
,在上述状态方程约束和初始条件下使泛函取值极小。12
特别地,当
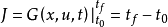 时,这就是最速控制问题。即以最短时间将系统的状态从初始点
时,这就是最速控制问题。即以最短时间将系统的状态从初始点
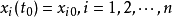 控制转移到指定的终端式
控制转移到指定的终端式

波尔扎问题给定一组微分方程式
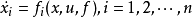 和初始条件式
和初始条件式
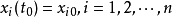 及某些终端条件式
及某些终端条件式
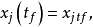 这与麦耶尔问题是一样的。要求的系统目标函数泛函为:
这与麦耶尔问题是一样的。要求的系统目标函数泛函为:
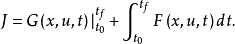
波尔扎问题要求从可供选择的函数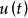 中确定出一个
中确定出一个 ,在满足约束条件、初始条件和终端条件下,使泛函
,在满足约束条件、初始条件和终端条件下,使泛函 取极小值。2
取极小值。2
泛函三种典型问题对比从上述三个问题的陈述中可以看出,它们的主要区别在于目标函数泛函不同。拉格朗日问题是一个积分指标,麦耶尔问题是一个终端时刻某一函数的取值,而波尔扎问题的目标函数泛函是前述两者之和,所以它更具一般性。但是,这三类问题之间又可以互相转化、所以实际上只是一类问题。21
本词条内容贡献者为:
李嘉骞 - 博士 - 同济大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国