学生t检验(英语:Student's t-test)是指虚无假设成立时的任一检定统计有学生t-分布的统计假说检定,属于母数统计。学生t检验常作为检验一群来自正态分配母体的独立样本之期望值的是否为某一实数,或是二群来自正态分配母体的独立样本之期望值的差是否为某一实数。举个简单的例子,也就是说我们可以在抓取一个班级的男生,去比较该班与全校男生之身高差异程度是不是推测的那样,或是不同年级班上的男生身高的差异的场合是否一如预期使用此检验法。
由来学生t检验是威廉·戈塞为了观测酿酒品质于1908年所提出的,“学生”则是他的笔名。基于克劳德·健力士(Claude Guinness)聘用从牛津大学和剑桥大学出来的最好的毕业生,以将生物化学及统计学应用到健力士工业流程的创新政策,戈斯特受雇于都柏林的健力士酿酒厂担任统计学家。戈斯特提出了t检验以降低啤酒质量监控的成本。戈斯特于1908年在《Biometrika》期刊上公布t检验,但因其老板认为其为商业机密而被迫使用笔名,统计学论文内容也跟酿酒无关。实际上,其他统计学家是知道戈斯特真实身份的。1
今日,它更常被应用于小样本判断的置信度。
应用最常用t检验的情况有:
单样本检验:检验一个正态分布的总体的均值是否在满足零假设的值之内,例如检验一群军校男生的身高的平均是否符合全国标准的170公分界线。
双样本检验:其零假设为两个正态分布的总体的均值之差为某实数,例如检验二群人的身高之平均是否相等。这一检验通常被称为学生t检验。但更为严格地说,只有两个总体的方差是相等的情况下,才称为学生t检验;否则,有时被称为Welch检验。以上谈到的检验一般被称作“未配对”或“独立样本”t检验,我们特别是在两个被检验的样本没有重叠部分时用到这种检验方式。
“配对”或者“重复测量”t检验:检验同一统计量的两次测量值之间的差异是否为零。举例来说,我们测量一位病人接受治疗前和治疗后的肿瘤尺寸大小。如果治疗是有效的,我们可以推定多数病人接受治疗后,肿瘤尺寸应该是变小了。
检验一条回归线的斜率是否显著不为零。
前提假设大多数的t检定之统计量具有t=Z/k的形式,其中Z与k是已知资料的函数。Z通常被设计成对于对立假说有关的形式,而k是一个尺度参数使t服从于t分布。以单样本t检验为例,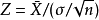 ,其中
,其中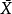 为样本平均数,n为样本数,
为样本平均数,n为样本数,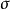 为总体标准差。至于k在单样本t检验中为
为总体标准差。至于k在单样本t检验中为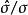 ,其中
,其中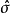 为样本的标准偏差。在符合零假说的条件下,t检定有以下前题:
为样本的标准偏差。在符合零假说的条件下,t检定有以下前题:
Z服从标准正态分布
(n-1)k服从自由度(n-1)的卡方分布
Z与k互相独立
单样本t检验检验零假说为一群来自正态分配独立样本xi之母体期望值μ为μ0可利用以下统计量
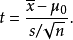
其中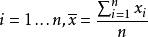 为样本平均数,
为样本平均数,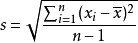 为样本标准偏差,n为样本数。该统计量t在零假说:μ=μ0为真的条件下服从自由度为n−1的t分布。
为样本标准偏差,n为样本数。该统计量t在零假说:μ=μ0为真的条件下服从自由度为n−1的t分布。
配对样本t检验配对样本t检验可视为单样本t检验的扩展,不过检验的对象由一群来自正态分配独立样本更改为二群配对样本之观测值之差。
若二群配对样本x1i与x2i之差为di=x1i−x2i独立且来自正态分配,则di之母体期望值μ是否为μ0可利用以下统计量
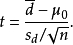
其中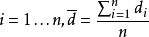 为配对样本差值之平均数,
为配对样本差值之平均数,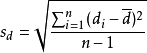 为配对样本差值之标准偏差,n为配对样本数。该统计量t在零假说:μ=μ0为真的条件下服从自由度为n−1的t分布。
为配对样本差值之标准偏差,n为配对样本数。该统计量t在零假说:μ=μ0为真的条件下服从自由度为n−1的t分布。
独立双样本t检验样本数及方差相等
若二群独立样本x1i与x2i具有相同之样本数n,并且彼此独立及来自二个方差相等的正态分配,则二群母体之期望值差μ1-μ2是否为μ0可利用以下统计量
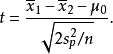
该统计量t在零假说:μ1-μ2=μ0为真的条件下服从自由度为2n−2的t分布。
样本数不相等但方差相等
若二群独立样本x1i与x2j具有不相同之样本数n1与n2,并且彼此独立及来自二个方差相等的正态分配,则二群母体之期望值之差μ1-μ2是否为μ0可利用以下统计量
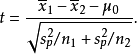
该统计量t在零假说:μ1-μ2=μ0为真的条件下服从自由度为n1+n2−2的t分布。
样****本数及方差皆不相等
若二群独立样本x1i与x2j具有相等或不相同之样本数n1与n2,并且彼此独立及来自二个方差不相等的正态分配,则二群母体之期望值之差μ1-μ2是否为μ0可利用以下统计量
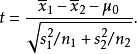 该统计量t在零假说:μ1-μ2=μ0为真的条件下服从自由度为
该统计量t在零假说:μ1-μ2=μ0为真的条件下服从自由度为
 之t分布。这种方法又常称为Welch检验。
之t分布。这种方法又常称为Welch检验。
电脑软件大多数的试算表软件及统计软件,诸如QtiPlot、OpenOffice.org Calc、LibreOffice Calc、Microsoft Excel、SAS、SPSS、Stata、DAP、gretl、R、Python、PSPP、Minitab等,都可以进行t检验之运算。
另请参阅方差齐性检验(F检验)
本词条内容贡献者为:
曹慧慧 - 副教授 - 中国矿业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国