[科普中国]-概率赋范线性空间

概率赋范线性空间是赋范线性空间的概念到概率度量空间情形的推广。

简介概率赋范线性空间是赋范线性空间的概念到概率度量空间情形的推广。

设E是实线性空间，𝒟为分布函数集，F:E→𝒟是映射。记Fx=F(x)及Fx(t)=(F(x))(t)。如果F满足下述条件：

1.Fx(0)=0(∀x∈E)；

2.Fx(t)=H(t)(∀t∈R)⇔x=0；

3.；

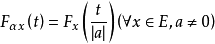4.设x,y∈E，t1,t2∈R，由Fx(t1)=1和Fy(t2)=1可推出，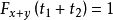

那么称(E,F)为一概率赋范线性空间，简称PN空间，这时F称为E上的概率范数。

推广在PN空间中，可定义概率度量为Fx,y=Fx-y，则它成为PM空间。1

概率度量空间（probabilistic metric space，简记为PM-空间）

概率度量空间亦称门杰概率度量空间，它是度量空间的一种重要推广，是指度量空间把两点间距离用一个统计量描述的一种空间。通常的度量取值于非负实数集，而概率度量取值于分布函数集。

1942年，K.Menger提出PM-空间以来，一直进展很慢，直到20世纪60年代，B.Schwweizer、A.sklar等研究了其拓扑结构，才使得这一理论有了较快的发展，但目前仍有大量的问题有待研究。

赋范线性空间赋范线性空间是在线性空间中引进一种与代数运算相联系的度量，即由向量范数诱导出的度量。赋范线性空间称为Banach空间，是指由范数导出的度量是完备的。

定义：设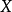是线性空间，函数称为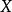上定义的一个范数，如果满足：

（1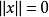）当且仅当；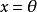

（2）对任何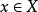及，；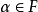

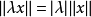（3）对任意，。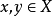

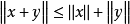称二元体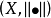为赋范线性空间。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学