[科普中国]-矢量势

向量微积分中，向量势（英语：vector potential），或称向量位，是一个向量场，其旋度为一给定向量场。这情形类比于标量势为一标量场，其负值梯度为一给定向量场。

简介向量微积分中，向量势（英语：vector potential），或称向量位，是一个向量场，其旋度为一给定向量场。这情形类比于标量势为一标量场，其负值梯度为一给定向量场。

形式上，给定一向量场v，则向量势为一向量场A使得

若一向量场v具有向量势A，则从等式

（旋度的散度为零）

可以得到

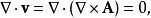
暗示了v必须是个螺线向量场(solenoidal vector field)。

一个有意思的问题是：是否任何螺线向量场都具有一向量势？答案是肯定的，只要向量势满足一些特定条件。1

非唯一性螺线向量场所具有的向量势不是唯一的。如果A是v的一个向量势，那么：

也是一个向量势，其中m是任何一个连续可微的标量函数。这可以从梯度的旋度是零的事实推出。1

参见向量分析基本定理

磁矢势

螺线管

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学