[科普中国]-多参考组态相互作用方法

多参考组态相互作用方法（multireference configuration interaction method，MRCI）是量子化学中的一种组态相互作用方法。

简介在该方法中，采用基态和部分激发态的电子组态斯莱特行列式作为参考态行列式，通过对所有的参考态行列式进行激发得到一组用于展开体系哈密顿量本征函数的多项式。仅包含所有单激发组态态函数作为参考态的 MRCI 方法称为单激发 MRCI（MRCIS），包含单激发和双激发的则称为 MRCISD，余类推。1

参考态方法对体系的基态而言，多参考态方法意味着更多的电子相关作用能的修正。非完全CI 方法的大小一致性问题在多参考态 CI 中并没有得到解决。

因为 MRCI 计算在电子相关上更大程度上平衡了基态与激发态，因此如果要通过 MRCI 方法来获得较为准确的激发能，那么在选择参考态的时候需要注意。特别地，如激发态主要由一个电子组态贡献，那么将该电子组态加入到参考态函数空间（简称“参考空间”）中就能得到较好的相关能修正，能够解决 CIS 和 CISD 方法过高估计激发能的问题，但是如果有几个电子组态对激发态的贡献都比较大，则仅仅把其中一个电子组态引入到参考空间中，仍然无法得到准确的激发能。

参考态函数的选取有三种方法：人工选取，自动选取（例如，选取一组分子轨道作为活性轨道，从基态出发进行所有仅仅涉及活性分子轨道的激发得到一组行列式作为参考态）、半自动选取（例如，选择在先前进行的 CI 或 MRCI 计算结果中贡献较大的行列式作为参考态）。2

组态相互作用方法组态相互作用方法(CI) 是一种后Hartree-Fock方法，求解的是多电子体系在波恩-奥本海默近似下的非相对论薛定谔方程。“构型相关”有两层含义：“构型" 从数学角度简洁的表述了它是描述波函的斯雷特行列式的线性耦合。根据轨道占据的规则 (例如, (1s)(2s)(2p)...)，“相关”的意思是不同电子构型（态）之间的混合（相互作用）。由于CI计算的CPU计算时间很长以及需要巨大的硬件资源，所以这个方法只能用于相对较小的体系。

与Hartree-Fock方法相比，为了计入电子相关作用，CI方法使用了由组态态函数（CSF）线性耦合得到的变分波函数，而这些组态态函数是由自旋轨道（用上标SO表示）构建的。

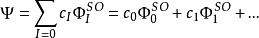
在这里， Ψ通常是指体系的电子基态。如果展开项包括了合适对称性的所有可能的 CSF, 则就是完全组态相互作用，它可以准确的求解由单粒子基组限定的空间内的电子薛定谔方程。上述展开项中的第一个就是Hartree-Fock行列式. 其他的构型态函数可以通过虚轨道和Hartree-Fock行列式中的自旋轨道交换的数目来表征。如果仅有一个自旋轨道不一样，我们就称它为单激发行列式。如果有两个自旋轨道不一样，就是双激发行列式，其余的以此类推。例如，CID方法只包含双重激发项，CISD方法包含单激发和双激发项。单激发项不和Hartree-Fock行列式混合。很多标准的程序中都有CID和CISD方法。戴维森校正可以被用于评估相对于CISD能量的矫正以说明更高的激发。2

本词条内容贡献者为:

曹慧慧 - 副教授 - 中国矿业大学