[科普中国]-纯量势

标势或称标量位，在矢量分析与物理学中是一个基本概念（形容词“标量”常被省略，只要不会与矢势发生混淆）。

简介标势或称标量位，在矢量分析与物理学中是一个基本概念（形容词“标量”常被省略，只要不会与矢势发生混淆）。给定一矢量场F，其标势V为一标量场；对此标量场取负值梯度则得到F：

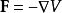
相反过来，给定一函数V，这个式子定义了一个矢量场F，其标势为V。标势也常常标记为希腊字母Φ，比如在电动力学的场合。

标势的物理意义和场的类型有关。对一流体或气体流的矢量场，定义标势暗示了任一点的流向与该点标势的最陡降方向相同，而对于力场，在一点的加速度也是一样的情况。力场的标势跟力场的势能（或称势能）密切相关。

不是每个矢量场都有一标势；有标势的矢量场称作是保守矢量场，相应于物理学中保守力的称呼。在各种速度场中，任何的层状场（lamellar field）皆有一标势，而一螺线矢量场可有标势的情况只发生在拉普拉斯场（Laplacian field）。1

向量分析向量分析（或向量微积分）是数学的分支，关注向量场的微分和积分，主要在3维欧几里得空间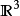中。“向量分析”有时用作多元微积分的代名词，其中包括向量分析，以及偏微分和多重积分等更广泛的问题。向量分析在微分几何与偏微分方程的研究中起着重要作用。它被广泛应用于物理和工程中，特别是在描述电磁场、引力场和流体流动的时候。

向量分析从四元数分析发展而来，由约西亚·吉布斯和奥利弗·黑维塞于19世纪末提出，大多数符号和术语由吉布斯和黑维塞在他们1901年的书《向量分析》中提出。向量演算的常规形式中使用外积，不能推广到更高维度，而另一种几何代数的方法，它利用可以推广的外积。1

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学