[科普中国]-波波夫稳定判据

在频率域内，由系统的线性部分的频率特性直接分析非线性单变量系统稳定性的判据。

定义在频率域内，由系统的线性部分的频率特性直接分析非线性单变量系统稳定性的判据。使用这样的判据分析非线性系统稳定性的方法称为波波夫法，它仅适用于能将系统中的非线性和线性部分分开的非线性系统。

设非线性系统如图1所示。系统中非线性特性y=f(x)可具有任意形式，但必须满足下列条件

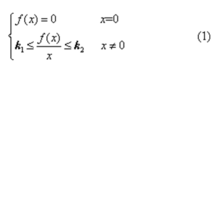
式中x为非线性部分的输入;f(x)为非线性部分的输出;k1，k2为将非线性特性f(x)夹在中间的两条直线的斜率，k2可为任意正值或无穷大，要求k1≥0。

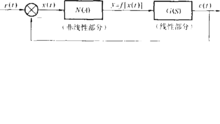
图1 非线性系统

设非线性系统中线性部分的全部极点具有负实部，其频率特性为G(jω)，再令

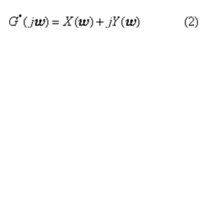
式中

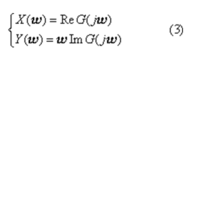
则作为波波夫稳定判据的非线性控制系统大范围渐近稳定的充分条件为

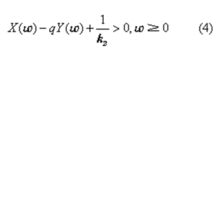
式中 q为某有限数。

如果令

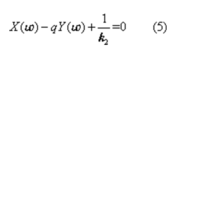
则式(5)代表一条在G*(jω)平面上通过点(-1/k2，j0)，斜率为1/q的直线，称此线为波波夫直线，如图2中的直线(1)。

波波夫稳定判据第一法若系统的G*(jω)轨迹线，对于所有ω≥0，均位于波波夫直线右侧，则此非线性系统为大范围渐近稳定的。

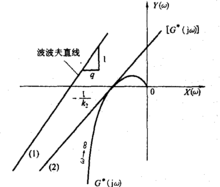
图2 波波夫稳定判据图解之一

通过G*(jω)轨迹线和负实轴的交点作与G*(jω)相切的切线，如图2中直线(2)。如果整个G*(jω)轨迹线位于此切线右侧，则由此切线表示的波波夫直线将给出保证系统大范围渐近稳定时的最大k2值。

由于G*(jω)轨迹线的形状不同，q的数值可以为q>0，或q