[科普中国]-弱微分

在数学中，弱微分是一个函数的微分（强微分）概念的推广，它可以作用于那些勒贝格可积（Lebesgue Integrable）的函数，而不必预设函数的可微性（事实上大部分可以弱微分的函数并不可微）。

一个典型的勒贝格可积函数的空间是L1([a,b])。在分布中，可以定义一个更一般的微分概念。

定义在数学中，弱微分是一个函数的微分（强微分）概念的推广，它可以作用于那些勒贝格可积（Lebesgue Integrable）的函数，而不必预设函数的可微性（事实上大部分可以弱微分的函数并不可微）。

命u是一个在 中的勒贝格可积的函数，称v 是u的一个弱微分，如果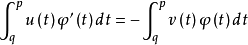，其中 是任意一个连续可微的函数，并且满足 。

推广到n维的情形，如果u和v是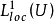 中的函数（在某个开集U中局部可极，U是 的子集），并且 是一个多重指标，那么v称为u的 次弱微分，如果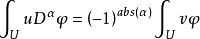 ，其中 是一个任意给定的函数，即给定的支撑集含于U的无穷可微的函数。

如果u的弱微分存在，一般被记为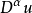 。可以证明，一个函数的弱微分在测度意义是唯一的，即如果有两个不同的弱微分，其仅可能在一个零测集上存在差异。

实例函数u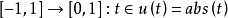： 在t=0并不可微，但具有以下被称为符号函数的弱微分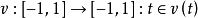： ，t>0时v(t)=1，t=0时v(t)=0，t