[科普中国]-勒雷一绍德尔不动点定理

勒雷-绍德尔不动点定理是用来证明拟线性椭圆方程边值问题有解的一个重要定理。

简介勒雷-绍德尔不动点定理是用来证明拟线性椭圆方程边值问题有解的一个重要定理。

设X是巴拿赫空间，T是从X×[0,1]到X中的紧映射，对所有的x∈X，使得T(x,0)=0。假设存在常数M，使得对满足x=T(x,σ)的所有(x,σ)∈X[0,1]，有||x||x0，存在一个不依赖于u和σ的常数M，使得狄利克雷问题：在Ω中Qσu=0，在∂Ω上u=σφ(0≤σ≤1)的每一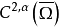解满足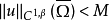。那么狄利克雷问题：在Ω中Qu=0，在∂Ω上u=φ在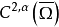中是可解的。1

本词条内容贡献者为:

杨荣佳 - 教授 - 河北大学