[科普中国]-格拉姆-施密特正交化过程

把线性无关向量系进行正交化的过程，称为格拉姆-施密特正交化过程。

简介正交化正交化是指将线性无关向量系转化为正交系的过程。

设{xn}是内积空间H中有限个或可列个线性无关的向量，则必定有H中的规范正交系{en}使得对每个正整数n（当{xn}只含有m个向量，要求n≤m），xn是e1,e2,…,en的线性组合。

定义这种把线性无关向量系进行正交化的过程，称为格拉姆-施密特正交化过程。1

正交系设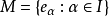 是内积空间H的一些非零元素构成的子集，若M中任何两个不同元素都正交，则称M为H中的一个正交系，进一步，若在正交系M中每个元素的范数均为1，则称M为H的一个标准正交系。

规范正交系设M是内积空间X的一个不含零子集，若M中向量两两正交，则称M为X中的正交系，又若M中向量的范数都为1，则称M为X中的规范正交系。

元素的正交性在内积空间和Hilbert空间中扮演着十分重要的角色。在n维欧氏空间，选定n个相互正交的向量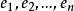，则形成n维空间中的一组正交基，也就是说在空间中建立了一组坐标系，空间中的任何一个元素都可以由这组坐标的线性组合表示出来。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学