[科普中国]-图灵归约

图灵归约是可计算性理论中的一种归约。

简介图灵归约是可计算性理论中的一种归约，若问题A可图灵归约成问题B，是指若问题B的解答已经知道（Rogers 1967, Soare 1987），就可以解问题A，也可以解释为若一个算法可以用来处理问题B，就可以处理问题A。较正式的说法，可被图灵归约成问题B的问题是指若存在问题B的预言机，就可以求解的问题集合。图灵归约可以用在决定性问题及功能性问题。1

图灵机的可计算性理论我们考虑关于图灵机的可计算性理论。本节中，固定字符集是{0, 1}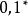，是所有有限长度字符串的集合。一个语言即是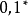的一个子集。

一个语言L是可以被图灵机所枚举（enumerate）的，如果存在一个图灵机 M，使得输入是L中的串时，M输出“接受”；而对非L中的串，M输出“拒绝”或不停机。而一个语言L'是可以被图灵机所决定（decide）的，如果存在一个图灵机M'，使得输入是L中的串时，M输出“接受”；而对非L中的串，M输出“拒绝”。注意这里的区别在于，对于图灵机决定的语言，我们需要在所有输出上，该图灵机都要停机。

可计算性等级这样我们可以定义可计算性等级：所有的语言的集合，记为All；递归可枚举语言，即可以被图灵机枚举的语言的集合，记为RE；递归语言，即可以被图灵机决定的语言的集合，记为R。可见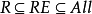，即形成可计算性等级。那么产生相关的问题即是两个包含关系是不是严格的，即是否有在All而不在RE中的语言，以及在RE而不在R中的语言。阿兰·图灵在1930年代的工作表明这两个包含关系都是不严格的，即可以证明存在语言L_d，是不能被图灵机所枚举的，以及存在语言L_u，是不能被图灵机所决定的。证明的主要思想是对角线法。

停机问题停机问题就是判断任意一个程序是否会在有限的时间之内结束运行的问题。该问题等价于如下的判定问题：给定一个程序P和输入w，程序P在输入w下是否能够最终停止。

PCP问题Post对应问题（Post's correspondence problem）。

不可解度不可解度的概念定义了不可解的集合之间的相对计算难度。例如，不可解的停机问题显然比任何可解的集合都要难，然而同样不可解的“元停机问题”（即所有具备停机问题的预言机的停机问题）却要难过停机问题，因为具备元停机问题的预言机可以解出停机问题，然而具备停机问题的预言机却不能解出元停机问题。

归约在可计算性理论与计算复杂性理论中，所谓的归约是将某个计算问题转换为另一个问题的过程。可用归约法定义某些问题的复杂度类（因转换过程而异）。

以直觉观之，如果存在能有效解决问题B的算法，也可以作为解决问题A的子程序，则将问题A称为“可归约”到问题B，因此求解A并不会比求解B更困难。

一般写作A ≤mB，通常也在≤符号下标使用的归约类型（m：映射缩小，p：多项式缩减）。

将一组问题归约到特定类型所产生的数学结构，通常形成预序关系，其等价类可用于定义求解难度和复杂度。

本词条内容贡献者为:

张尉 - 副教授 - 西南大学