[科普中国]-高斯-勒让德算法

高斯-勒让德算法是一种用于计算π的算法。它以迅速收敛著称，只需25次迭代即可产生π的4500万位正确数字。不过，它的缺点是内存密集，因此有时它不如梅钦类公式使用广泛。

介绍高斯-勒让德算法是一种用于计算π的算法。它以迅速收敛著称，只需25次迭代即可产生π的4500万位正确数字。不过，它的缺点是内存密集，因此有时它不如梅钦类公式使用广泛。

该方法基于卡尔·弗里德里希·高斯（1777–1855）和阿德里安-马里·勒让德（1752–1833）的个人成果与乘法和平方根运算的现代算法的结合。该算法反复替换两个数值的算术平均数和几何平均数，以接近它们的算术-几何平均数。

下文的版本也被称为高斯-欧拉，布伦特-萨拉明（或萨拉明-布伦特）算法；它于1975年被理查德·布伦特和尤金·萨拉明独立发现。日本筑波大学于2009年8月17日宣布利用此算法计算出π小数点后2,576,980,370,000位数字，计算结果用波温算法检验。1

知名的计算机性能测试程序Super PI也使用此算法。

算法设置初始值：

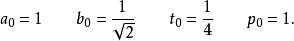
反复执行以下步骤直到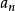 与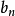 之间的误差到达所需精度：

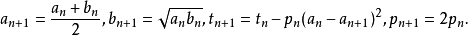
则π的近似值为：

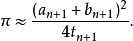
下面给出前三个迭代结果（近似值精确到第一个错误的位数）：

3.140...

3.14159264...

3.1415926535897932382...

该算法具有二阶收敛性，本质上说就是算法每执行一步正确位数就会加倍。

数学背景算术-几何平均数的极限a0和b0两个数的算术-几何平均数，是通过计算它们的序列极限得到的：

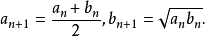
两者汇聚于同一极限。
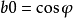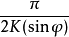若 a0=1且，则极限为，其中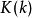为第一类完全椭圆积分：

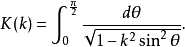
若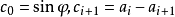，则

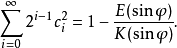
其中E(k)为第二类完全椭圆积分：

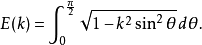
高斯知道以上这两个结果。

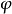勒让德恒等式对于满足的与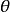，勒让德证明了以下恒等式：

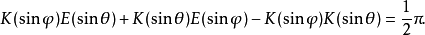
高斯-欧拉法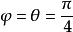的值可以代入勒让德恒等式，且K、E的近似值可通过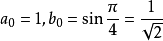的算术-几何平均数的序列项得到。

本词条内容贡献者为:

张尉 - 副教授 - 西南大学