[科普中国]-里斯-菲舍尔定理

里斯-菲舍尔定理是贝塞尔不等式的逆命题，里斯(Riesz,F.)和菲舍尔(Fischer,E.S.)于1907年最早对特殊的希尔伯特空间L2[0, 2π]和规范正交系证明了这个定理。

简介里斯-菲舍尔定理是贝塞尔不等式的逆命题。

设 是希尔伯特空间H中的规范正交系，F张成的闭子空间为E；又设是一族数，满足

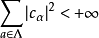则必存在惟一的向量x∈E，使x关于{eα}的傅里叶系数是{cα}，即cα=(x,eα)，且

这一结论通常称为里斯-菲舍尔定理。

发展里斯(Riesz,F.)和菲舍尔(Fischer,E.S.)于1907年最早对特殊的希尔伯特空间L2[0, 2π]和规范正交系

证明了这个定理。1

贝塞尔不等式贝塞尔不等式是类似于勾股定理的一种不等式。贝塞尔不等式揭示了希尔伯特空间中的一个元素和它在一个正交序列上的投影之间的关系。

举例来说，平面上的一个向量的长度的平方等于它在两个相互垂直的坐标轴上的投影的平方和，而对于一个三维空间上的向量，它在两个相互垂直的坐标轴上的投影的平方和一般会小于它自身的长度的平方，除非它就在这两个坐标轴构成的平面上。对于一个希尔伯特空间中的向量来说，它在任意一个正交序列上的投影的平方和也是小于等于它自身的长度的平方。这就是贝塞尔不等式。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学