[科普中国]-德窖特茨基-罗杰斯定理

巴拿赫空间中的无条件收敛级数为绝对收敛的充分必要条件是该空间为有限维的，这就是著名的德窖特茨基-罗杰斯定理。

简介设X为巴拿赫空间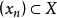，，若对任何ε>0，存在正整数N，使当m>n≥N时

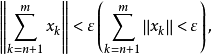
则称级数

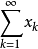收敛（绝对收敛）。如果对正整数集的每个重排π，级数

都是收敛的，就称级数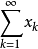是无条件收敛的。显然，级数的绝对收敛性蕴涵无条件收敛性。

巴拿赫空间中的无条件收敛级数为绝对收敛的充分必要条件是该空间为有限维的，这就是著名的德窖特茨基-罗杰斯定理。1

无条件收敛级数（unconditionally convergentseries）

无条件收敛级数主要包括数值级数的无条件收敛和Banach空间内级数的无条件收敛，两者的定义是相同的，是指任何重排均收敛的级数。换句话说，无条件收敛级数是这样的级数：不管如何交换它的项的次序，所得到的级数仍然收敛，因此，又称可换收敛级数。对数项级数而言，级数是无条件收敛的当且仅当级数是绝对收敛等价的。无穷维空间内的无条件收敛主要包括Hilbert空间内的无条件收敛、Lp空间内的无条件收敛、一致凸Banach空间内的无条件收敛、cotype p的Banach空间内的无条件收敛级数。

绝对收敛绝对收敛一般用来描述无穷级数或无穷积分的收敛情况。如果级数ΣUn各项的绝对值所构成的级数Σ|Un|收敛，则称级数ΣUn绝对收敛，级数ΣUn称为绝对收敛级数。绝对收敛级数一定收敛。

若函数f(x)在[a,b]上可积，且|f(x)|的无穷积分（从a到+∞）上收敛，则称 f(x) 的无穷积分（从a到+∞）绝对收敛。绝对收敛一定收敛。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学