[科普中国]-增生映射

增生映射是单调映射在自映射情形的变种。在希尔伯特空间中，增生映射与单调映射是同一概念。

简介增生映射是单调映射在自映射情形的变种。

设 X 是巴拿赫空间，D⊂X，T:D→X，设映射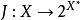 是由下式定义的正规对偶映射

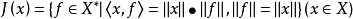若T 满足条件：对任意对x,y∈D，存在 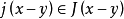使得

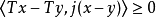则称 T 为增生映射。1

单调映射单调映射是单调递增一元函数概念在对偶作用意义下的无穷维推广。

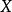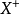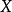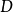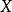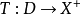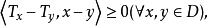设是巴拿赫空间，为的对偶空间，⊂，，若有则称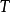为单调映射。若等号仅当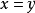时成立，则称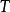为严格单调映射。

若存在连续函数

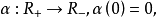
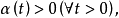
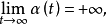使得

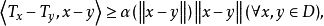则称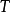为强单调映射。

在希尔伯特空间中，增生映射与单调映射是同一概念。

对偶映射(dual mapping)

对偶映射是线性代数中共轭变换的推广。

设E*，E与F*，F是对偶空间，φ是E到F的线性映射，φ*是F*到E*的线性映射。若对任意x∈E，y*∈F*，有：

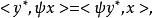则称φ与φ*是一对对偶映射。

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院