[科普中国]-抽象柯西问题

抽象柯西问题是以向量值函数为解的微分方程的初值问题。算子半群理论和抽象柯西问题与马尔可夫过程有很密切的联系。

简介抽象柯西问题是以向量值函数为解的微分方程的初值问题。

设A是巴拿赫空间X上的线性算子，定义域是𝓓(A)，y0∈X，是否有取值于X上的向量值函数y(t)，满足：

1、y(t)∈𝓓(A)(t>0)，在任何[α,β]⊂(0,+∞)上强可导。

2、。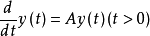

3、。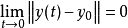

此问题称为抽象柯西问题。

解如有y(t)满足抽象柯西问题的1-3条件，则称y(t)是方程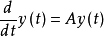适合柯西条件y(0)=y0的解。

应用通常的热传导方程、薛定谔方程，以及用矩阵表示的波动方程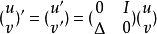都可纳入抽象柯西问题。

用算子半群为工具研究上述抽象柯西问题可得到如下结构：设A是C0类算子半群{Tt|t≥0}的无穷小生成元，则方程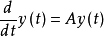的抽象柯西问题对每个y0∈𝓓(A)有惟一解Tty0。

算子半群理论和抽象柯西问题与马尔可夫过程有很密切的联系。1

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院