[科普中国]-希尔-吉田耕作定理

希尔-吉田耕作定理是给出某个C0类算子半群生成元的充分必要条件的定理。

简介希尔-吉田耕作定理是给出某个C0类算子半群生成元的充分必要条件的定理。

希尔-吉田耕作定理是半群理论的最基本定理之一，它有多种表示形式。

内容设A是巴拿赫空间X上的稠定线性算子，则A是X上的某个C0类算子半群{Tt|t≥0}的无穷小生成元的充分必要条件是：存在常数M,β和实数列λn→+∞，满足：

1、当λn>β时，(λnI-A)-1是有界线性算子；

2、对任何m，当λn>β时，上述命题称为希尔-吉田耕作（算子半群）定理。1

C0类算子半群C0类算子半群是一类具有强连续性的算子半群。

设X是复的局部凸拓扑线性空间，L(X)表示X上的连续线性算子全体。如果L(X)的算子族{Tt|t≥0}满足条件：

1、TsTt=Ts+t(s,t∈[0,+∞),T0=I)；

2、（强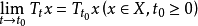），则称{Tt|t≥0}为C0类算子半群，简称C0类半群。

当X是巴拿赫空间时，对C0类算子半群{Tt|t≥0}必存在M>0和β≥0，使得||Tt||≤Meβt(t≥0)。

例如X=Lp(-∞,+∞)(1≤p