[科普中国]-维纳-霍普夫积分方程

维纳-霍普夫积分方程是由于研究辐射迁移理论的需要而提出的一类积分方程，是实际应用中经常遇到的，但不完全满足古典的弗雷德霍姆理论的方程。

简介维纳-霍普夫积分方程是由于研究辐射迁移理论的需要而提出的一类积分方程。

下面的线性积分方程 称为维纳-霍普夫积分方程。

发展理论基础维纳-霍普夫积分方程是实际应用中经常遇到的，但不完全满足古典的弗雷德霍姆理论的方程。由于研究辐射迁移理论的需要，从20世纪20年代起就开始了对这一类型方程的研究。

关于方程

的第一个结果是1931年由维纳(Wiener,N.)与霍普夫(Hopf,H.)共同得到的。他们在假定核k(t)和未知函数q(t)满足一定的条件下，得到了方程的齐次方程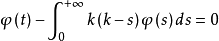解的解析表达式。

在维纳与霍普夫的上述工作中，第一次利用了因子分解的思想来处理方程。

由研究维纳-霍普夫方程而逐渐发展起来的维纳-霍普夫技巧（即因子分解的技巧），现在已经成为研究维纳-霍普夫方程的重要的理论基础，而且也是研究许多数学物理问题的强有力的工具。

发现联系关于方程的第二个重要结果是由拉普泼特于1948年得出的。他在假定核k(t)满足适当的条件，把方程化成一个黎曼边值问题，从而借助黎曼边值问题的一些熟知结果对方程进行研究。在上述工作中，拉普泼特建立了方程在函数类L2(0,+∞)中的正则可解性定理，并且第一次指出了指数

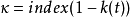与齐次方程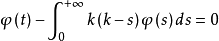的线性无关解个数之间的紧密联系。

完整化1958年，克列因和哥赫别格等人进一步发展了维纳-霍普夫的因子分解的思想，对方程建立了更为一般和更加完整的理论。1

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学