西尔维斯特方程(Sylvester equation)是控制理论中的矩阵方程。
定义西尔维斯特方程(Sylvester equation)是控制理论中的矩阵方程,形式如下:
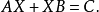
其中A、B及C是已知的矩阵,问题是要找出符合条件的X。其中所有矩阵的系数都是复数。为了要使方程成立,矩阵的行和列需要满足一定条件,A和B都要是方阵,大小分别是n和m,而X和C要是n行m列的矩阵,n和m也可以相等,四个矩阵都是大小相同的方阵。
西尔维斯特方程有唯一解X的充份必要条件是A和-B没有共同的特征值。
AX+XB=C也可以视为是(可能无穷维中)巴拿赫空间中有界算子的方程。此情形下,唯一解X的充份必要条件几乎相同:唯一解X的充份必要条件是A和-B的谱互为不交集。1
解的存在及唯一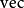 利用克罗内克积以及向量化量子,可以改写西尔维斯特方程为
利用克罗内克积以及向量化量子,可以改写西尔维斯特方程为
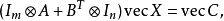
其中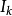 为
为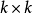 单位矩阵。在此形式下,可以将问题改为
单位矩阵。在此形式下,可以将问题改为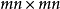 维的线性系统。
维的线性系统。
命题
假定复数的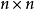 矩阵
矩阵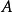 和
和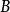 ,西尔维斯特方程针对任意
,西尔维斯特方程针对任意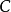 有唯一解,若且唯 若
有唯一解,若且唯 若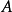 和
和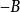 没有共同的特征值。
没有共同的特征值。
证明
考虑线性转换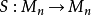 ,
,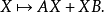
(i)假设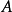 和
和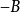 没有共同的特征值,则其特征方程式
没有共同的特征值,则其特征方程式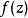 和
和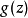 的最大公因式为
的最大公因式为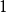 ,因此存在复数多项式
,因此存在复数多项式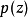 和
和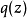 ,使得
,使得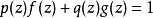 。依照Cayley–Hamilton定理,
。依照Cayley–Hamilton定理,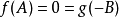 ;因此
;因此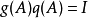 。令
。令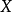 为
为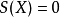 的解,则
的解,则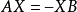 ,重复上述作法,可得
,重复上述作法,可得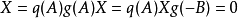 。因此依照秩-零化度定理,
。因此依照秩-零化度定理,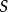 是可逆的,因此针对所有的
是可逆的,因此针对所有的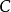 都存在唯一的解
都存在唯一的解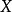 。
。
(ii) 相对的,若假设 是
是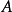 和
和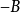 的共同特征值,则
的共同特征值,则 也是
也是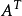 的特征值。存在非零向量
的特征值。存在非零向量 和
和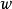 使得
使得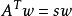 以及
以及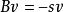 。选择
。选择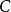 使得
使得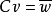 ,向量的元素是
,向量的元素是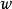 的共轭复数,则
的共轭复数,则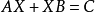 没有解
没有解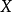 ,因为复数的双线性pairing
,因为复数的双线性pairing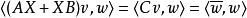 ,等号的右边为正值,而左侧为零。2
,等号的右边为正值,而左侧为零。2
Roth消去法则假设二个大小分别为n和m的方阵A和B,以及大小为n乘m的矩阵C,则可以确认以下二个大小为n+m的方阵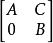 和
和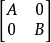
是否彼此相似。这二个矩阵相似的条件是存在一矩阵X使得AX-XB=C,换句话说,X为西尔维斯特方程的解,这称为Roth消去法则(Roth's removal rule)。
可以用以下方式检查,若AX-XB=C,则
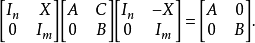
Roth消去法则无法延伸到巴拿赫空间中的无穷维有界算子中。1
数值解西尔维斯特方程数值解的经典算法是Bartels–Stewart算法,利用QR算法将矩阵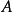 和矩阵
和矩阵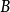 转换为舒尔形式,再用逆向取代法求解三角矩阵。此算法若用LAPACK计算,或是GNU Octave的lyap函数计算,计算复杂度是
转换为舒尔形式,再用逆向取代法求解三角矩阵。此算法若用LAPACK计算,或是GNU Octave的lyap函数计算,计算复杂度是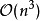 个数学运算。也可以参考其中的sylvester函数。在一些特定的影像处理应用中,西尔维斯特方程会有解析解。2
个数学运算。也可以参考其中的sylvester函数。在一些特定的影像处理应用中,西尔维斯特方程会有解析解。2
本词条内容贡献者为:
李斌 - 副教授 - 西南大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国