[科普中国]-亏指数

设A是复希尔伯特空间H中的对称算子，𝓡(A+iI)⊥和𝓡(A-iI)⊥称为A的亏子空间，记n+=dim𝓡(A+iI)⊥，n-=dim𝓡(A-iI)⊥，称数对(n+,n-)为A的亏指数。

简介亏指数是与对称算子有关的数对。

设A是复希尔伯特空间H中的对称算子，𝓡(A+iI)⊥和𝓡(A-iI)⊥称为A的亏子空间，记n+=dim𝓡(A+iI)⊥，n-=dim𝓡(A-iI)⊥（这里空间的维数指该空间中完备规范正交系的势），称数对(n+,n-)为A的亏指数。

判定A自伴的充分必要条件是n-=n+=0。

对称算子A具有自伴扩张的充分必要条件是n-=n+。1

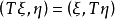对称算子设T是作用在希尔伯特空间H上的稠定算子，如果对任意有。亦即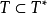，则称T是对称算子。

每个对称算子都有闭的对称扩张。如果对称算子T没有真的对称扩张，即若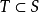且S是对称算子一定有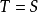成立时，则称T是极大对称的（maximally symmetric ）。

在一定条件下，对称算子与等距算子可通过凯莱变换相互转化。

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院